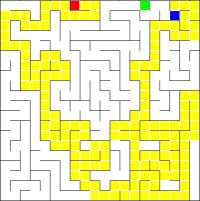
|
Practical algorithms and code optimization: maze generation |
The present document is published under terms of the "Verbatim Copying » as defined by the Free Software Fondation within the scope of the GNU project.
Verbatim copying and distribution of this entire article is permitted (and encouraged) in any medium without royalty provided this notice is preserved.
Copyright (C) 2003, 2004 Yann LANGLAIS, ilay.
The last version of this document is located at the folling URL:
http://ilay.org/yann/articles/maze/index.en.html
Any remarque, suggestion or correction is welcomed and can be addressed to
Yann LANGLAIS,
ilay.org.

Let's start by opening the dictionnary:
labyrinth: n place constructed of or full of passageways and blind alleys: maze
maze: n: a confusingly intricate network of passages.
If these definitions are enough to allow comprehension of the concept, they are useless for creating a program.
A maze is a conected surface. Such surfaces may have different topologies: simple, or with rings or islands.

|

|
| Simple connected surface | Connected Surfaces with rings |
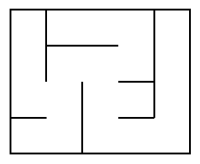
These two surfaces are not topoligically equivalent. The difference, in the case of mazes leads to different maze types: perfect mazes and imperfect mazes.
Perfect mazes are made of a unique path connecting every cell (or pathway).
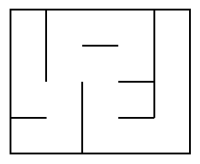
Imperfect mazes are made of a path that may intersect itself (non unique path) or/and isolate
a group of cells.
 |
 |
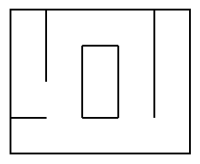 |
| Perfect maze | Imperfect mazes | |
We will only be conserned by perfect mazes.
The different paths of prefect maze can be viewed as a tree:
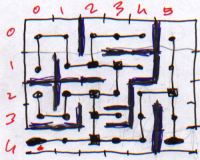 |
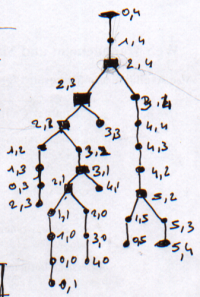 |
| Labyrinthe | Arbre équivalent |
A prefect rectangular maze of m columns and n lines is a set of m x n cells connected by a unique path.
Each cell is linked to all others by a unique path.
Topological equivalence of simple connected surfaces allow us to refine our vision of perfect mazes:
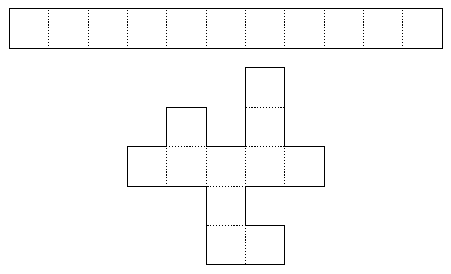 |
| Equivalent surfaces |
The number of opened doors required to define a unique path through any maze of mn is the same as the number of opend doors required in the case of a straight path of a single row of mn cells, that is mn - 1 opened doors.
Le total number of possible internal doors is then: 2mn - m - n
We have two doors per cell (to avoid counting twice the same) on the down side and on the right side, for instance, minus the number of external bounding doors down side m and right side n.
The number of walls (or closed doors) of a perfect maze is then:
2mn - m - n - (mn - 1) = (m - 1) (n - 1)
A maze is composed of cells and doors. Both concept are somehow equivalents. Cells are bound by doors and the doors bind cells. We need to choose wich is concept we want to modelize.
Provided we wander through cells, it seems easer to me to think in terms of cells rather than doors.
At first sight and thinking of doors as links from one cell to another, we could code doors as pointers to other cells. Each cell would then be composed by 4 pointers. An open door from a cell to another would then be a plain pointer to the next cell and a closed door would be a null pointer.
This modelization works perfectly. But while taking a closer look to the problem, we don't need it. The doors of our maze is not a complex hyperspace with wormholes. We do not need to store data giving the position of next cell.
We only need to know the state of each door (open/close). Four doors bound each cell and each door has only two possible states. We then only need 4 bits per cell to code the states.
We will also probabily need to know if we already passed through a cell. We then have to add one bit per cell. Our cell will then use only 1 byte of data.
Beeing strict, this data representation is incorrect since each door state is coded twice (once
in 2 neighbourg cells limited by the door itself). A door is then completely opened if and
only if is opened in the 2 adjascent cells.
It would be better to store door state in only one cell. However, from a pracitcle stand point,
the redondant code only account for 2 extra bits, wich is few since the "minimal" size of a
variable is the byte. Furthermore, the time consumed to open twice the same door is also really small.
Subdividing a byte in 2 to code 2 cells per byte would raise complexity and would probably not save computation time.
The maze in itself is a set of mn cells. We need to store m, n and the cells. We also need to take into account the entrance and the exit.
Storing the cells is an important issue. Since the maze is a rectangle, an 2-dimensional array should be fine.
However, this way has 2 inconvinients:
A 2-dimensional array can also be represented as a vector of the same number of cells. The translation from a 2D coordinates system to a single coordinate system is obvious provided we know the dimensions of the 2D space:
|
x, y -> i : i = my + x i -> x, y : x = i / m et y = i % m * |
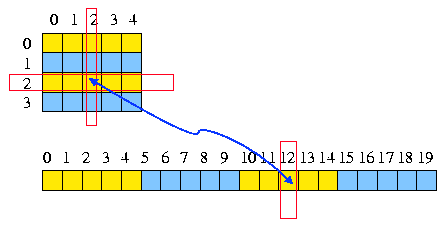 |
* thus respectively, the result of an integer division by m and the modulus of this division.
This way, we have addressed the 2 previous inconvinients.
Recap:
A cell is coded on 1 char (i.e. 1 byte).
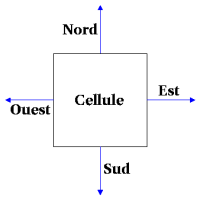
We can name the 4 doors North, West, South and East.
North will be bit 0, West bit 1, South bit 2, and East bit 3.
The state of the cell (visited/not visited) on bit number 4.
The maze contains the 2 integers m and n, the dimensions. The entrance and the exit will be coded by their index within the vector, or by pointers to the cells.
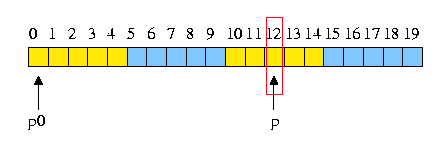
In the following, I'll use pointers since their wrinting is more consise than using indexes.
And we'll store the cells in a vector of characters.
We then have the following structure:
typedef struct _maze_t {
int m, n;
char *in, *out;
char *array;
} maze_t, *pmaze_t;
Considering that the best quality of a computer scientist is lazyness and since we are not supposed to reinvent the wheel each time, the first thing to do is to gather an analyse existing algorithms. Nothing prevent us from thinking on our own to the problem, but having a look to existing solutions is a good way to spare time.
We could have began by looking for existing solutions at the first place instead of thinking about data structures. But two good reasons have imposed me another approach. In one hand, data structure is a fondamental point, which needs a clean analysis, with no a priori if we want to make things simple and consise. This step is independent of the matter. It is the modelisation step. On the other hand, this particular subject of mazes seems to give problems to most of the programers who provided free implementations. Most of their data sturctures contain superfluous stuff.
After a query on my favorite search engine, I've identified two types of alogrithms.
This first type use a property of perfect mazes previously expressed: Each cell is connected to all others by a unique path.
This type sets a unique value to each cell (let say the cell index within the vector) and starts fom a maze where all doors are closed.
When a door is opened between two adjascent cells, two pointers are linking the cells both ways and the value of the first cell is affected to the second.
The connected cells become atoms of a doublely linked list. Each time a door is to be opened, one must check that the values on both side are different.
If the values are the same, it means that the two cells are already connected and that the door cannot be opened.
If the values are different, the door can be opened and te values on the other side are set to the one on the current side and propagated along the linked list.
The selection of doors is made randomly.
Let's see graphically how it works:
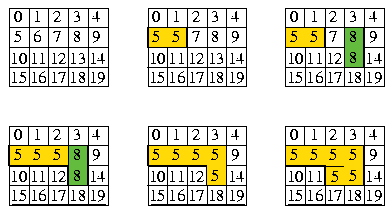
In the last picture, it is impossible to open the door between the cell initially numbered 7 and the cell intially numbered 12.
To complete the generation, we simply have make a loop which randomly tries to open a door until mn - 1 doors are opened.
This algorithm works fine but needs to implement doublely linked lists.
Half of those lists are also browsed entirely when each door is opened.
Moreover, since doors are selected randomly we cannot constrain the number of loops required to open all needed doors. Indeed, random mecanism may choose already opened doors or un openable doors an infinite number of times.
To address this issue, we have two alternatives:
However, these two solutions are unsatisfactory. The first in terms of determinism, performances and method. The second, in terms of complexity and performances.
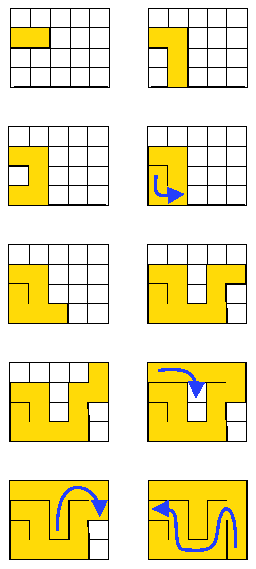
|
We start with a maze where all doors are clorsed Each cell contains a boolean variable called "state" telling whether the cell has been visited or not. All state variables initialized to False (0). We choose a cell, set its state to True (1). Then we look at adjascent cells to check if they've been visited or not. If at least one door may be opened, we choose randomly a door and open it. We move to the next cell and restart the process. If no door is available, whe regress until finding a cell with at least one door available and we restart the process. When no more door available, the maze is all done. |
The history of visited cells can be achieved in two ways:
Recursive code gives excellent results and does not require extra code. It is efficient for small or medium sized mazes. But when dealing with larger mazes such as 1000x1000 cells, the stack size might not suffice and the program might stack overflow. Since we have no ability to control the stack size runtime, a manual history shall ve prefered.
This algorithm is less complex than the previous. It does not need to implement complex structures.
The two methods are not qualitatively equivalent.
The first one gives a maze which representative tree is better balanced than the second.
Indeed, in the first case, all openable doors have equal probability of beeing chosen.
The first method will help bifurcations.
A contrario, the second help long paths. Representative trees will be unbalanced. The earlier the path is generated, the longer it is. The later it is generated and the shorter it is.
The final maze will be composed of few long paths and each of them will only have small branches.
For small sized mazes, the two methods will give comparable results. Bigger mazes will appear different.
Quantitively, the second method is averagely faster than the first. Time difference will also increase with the size of the mazes.
The second method is particularily easy to implement. It doesn't need complex structures. It is fully deterministic and consistent. Therefore, I consider it the best choice.
The code will be split in two files:
The complete package also include a X11 interface (X11.c and X11.h), a 'main" (main.c) and a Makefile to modify according to target configuration.
The file "maze.h" contains only 3 prototypes: constructor, solver and destructor.
Let see the different fonctions coded in maze.c.
The 4 directions (North, South, West and East) :
/* define directions: */
enum { N, W, S, E };
The following binary masks will help find the state of a door (e.g. state of south door will be given by "cell & CELL_S") :
/*
* Cell definitions:
* -----------------
* Cells are maped by chars.
* 1st bit maps North door
* 2nd bit maps West door
* 3rd bit maps South door
* 4th bit maps East door
* 5th bit maps visited cells.
*
* bit unset => closed or unvisited
* bit set => open or visited
*/
/* Bit masks: */
#define CELL_N 1
#define CELL_W 2
#define CELL_S 4
#define CELL_E 8
#define CSTATE 16
/* define maze structure */
typedef struct _maze_t {
/* maze size = m lines * n columns */
int m, n;
/* entrence and exit cells */
char *in, *out;
/* array of cells */
char *array;
} maze_t, *pmaze_t;
cell_x, cell_y : These fonctions return coordinates of a cell defined by its pointer.
Here is how they work:
cell_at_xy : returns the pointer to the cell of coordinates (x, y).
index = m * y + x
cell_at_dir : this function checks if a cell is located in a given direction. If a cell exist, its pointer is returned. Else, a null pointer is returned.
maze_rand : returns a number between 0 and n-1 given n.
maze_rand_border_cell : Choose randomly one cell on a border.
maze_new : this function returns a pointer to a new maze from its number of columns and lines plus an optional drawing function pointer. maze_new allocates and initializes the maeez, then generate it by calling cell_next.
The optionnal drawing function takes 3 integers corresponding to cell coordinates and the direction of he door to be opened.
maze_destroy : desallocate maze structure.
cell_next : cell_next implements the previously discussed maze generetion method.
It is made of 2 infinite loops. The innermost is responsible for growing the current path one step forward while the outermost goes one step backward within position history.
In the innermost, scells next to current cell are scanned. A list of possible next cells is built. Then the maze_rand(n) function choose 1 of the possibilities. The door between current cell and choosen cell is opened. This last operation is made as following:
cellule |= 1 << i
where i is the direction (N = 0, W = 1, S = 2, E = 3)
A char is initialized to 1 and w rotation of 'i' bits toward left.
For North door (N): 00000001
For West door (W): 00000010
For South door (S): 00000100
And for East door (E): 00001000
Applying an exclusive or to the cell to open corresponding door.
To obtain the same door within the next cell, we just have to add 2 modulo 4 to i.
The previous cell is added to position history and we restart the procces.
http://ilay.org/yann/articles/maze/maze.tgz
Here is a Flash applet, courtesy from Adrien Béraud, which illustrates the 2 algorithms :
And the sources of the flash program.

Think Labyrinth: Maze Algorithms http://www.astrolog.org/labyrnth/algrithm.htm
Maze generation algorithm (http://www.worldwidewebfind.com/encyclopedia/en/wikipedia/m/ma/maze_generation_algorithm.html
Xlockmore (http://www.tux.org/~bagleyd/xlockmore.html), module "maze"
Structures de données : Un labyrinthe en C++, Juan Barragan, Login numéro 105, avril 2003
Les labyrinthes, Rémi Peyronnet, http://www.via.ecp.fr/~remi/prog/algo.php3
Générateur de labyrinthe, Romain Vinot, http://www.chez.com/romanino/maze/maze.html
TD5 - C - Archivage, Récursivité et Labyrinthe, IUP2 - MIAGe, November 3, 2002, http://www.loria.fr/~barreaud/enseignement/TD5/TD5.html
INTRODUCTION A L'ALGORITHME, http://perso.club-internet.fr/assomasi/Sciences_Informatiques/Algorithmes/Introduction_Algorithme.html#Labyrinthes
Memory management in C, http://ilay.org/yann/articles/mem/
Advanded memory structures (doublely linked lists, btrees, hash coding, ...), http://ilay.org/yann/articles/
Other technical documents:
http://ilay.org/yann/articles/